ざっくり分かるファイナンス 経営センスを磨くための財務

サマリー&レビュー
内容
コーポレート・ファイナンスのミッション(企業価値の最大化)を果たすためのポイントについて記載されている。
コーポレート・ファイナンスの役割とポイント
- 投資の決定(資金調達コスト以上に利益を上げられる事業に投資する)
- 資金の調達(銀行と株主からの資金調達バランスを取りつつ、株主資本コストの低減に努める)
- 配当政策(成長が鈍化し、良い投資案件がなくなったら配当する)
対象者
- 一歩進んだファイナンスを学びたい人
難易度
- 初学者が「さっ」と一読しただけでは全貌を理解するのは厳しい
- 深読(何度も、じっくりと読む)をして、はじめて全貌を理解できる
- 本書だけではなく、ネットで適宜検索しつつ知識を補完する作業も必要
評価
★★★★★★(6/5)
- 「ざっくり」とファイナンスの重要なエッセンスを学べる良書
- 表面的なファイナンスの説明ではなく、生きたファイナンス(現場で揉まれた経験)を学べる
予備知識
この章では、この本のメイントピックである「コーポレート・ファイナンス」を理解するための前提知識である財務の基本事項をまとめる。
財務三表と財務鳥瞰図
決算書は下記財務三表で構成される。
| 項目 | 概要 |
|---|---|
| 貸借対照表(バランスシート) | どのように資金を調達しているか、その資金をどのように運用しているか |
| 損益計算書 | 利益や損失がどのくらいか |
| キャッシュフロー計算書 | 収入と支出がどれだけあったか |
賃借対照表
賃借対照表は、下記3項目で構成される。
| 項目 | 意図 | 内容 | 図中 |
|---|---|---|---|
| 資本 | 資金の調達方法 | 資本金、余剰金 | 点線 |
| 負債 | 資金の調達方法 | 借入金、社債、支払手形、買掛金 | 破線 |
| 資産 | 資金の運用方法 | 預金・現金、有価証券、有形固定資産、無形固定資産、棚卸資産、受取手形、売掛金 | 実践 |
財務鳥瞰図
損益計算書
 損益計算は、上記6項目により計算される。「営業利益」が「本業で儲ける力」を表しており、これは「事業に投資することによって得られたリターン」を表している。
損益計算は、上記6項目により計算される。「営業利益」が「本業で儲ける力」を表しており、これは「事業に投資することによって得られたリターン」を表している。
コーポレート・ファイナンス
この本のメイントピックである。ファイナンスのミッションは「企業価値の最大化」であり、3つの役割からなる。
| 役割 | 概要 |
|---|---|
| 投資の決定 | どの事業に投資するのか |
| 資金の調達 | どのように資金を調達するのか |
| 配当政策 | どのように配当を出すのか |
企業価値の最大化
企業価値とは
企業価値は下記式で求められる。
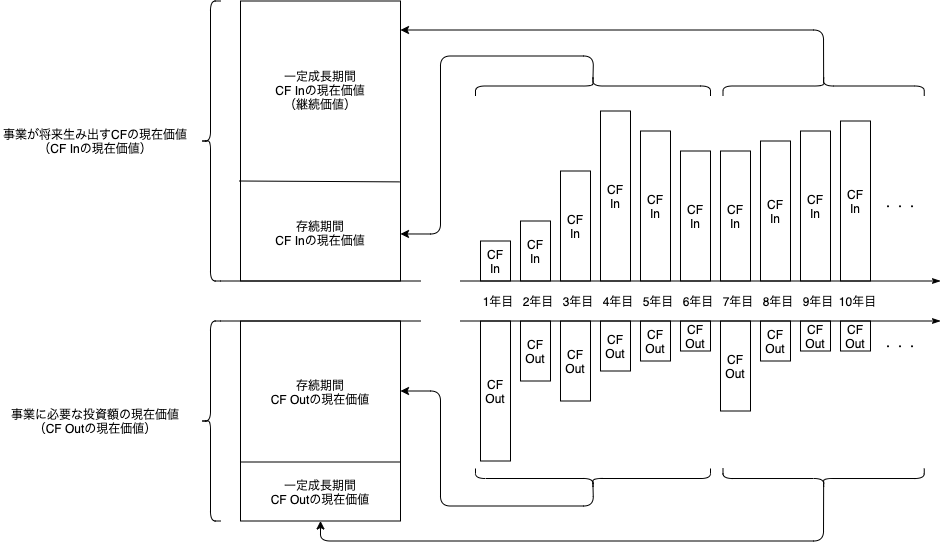
\[企業価値 = 事業価値 + 非事業価値\]事業価値は「その事業が将来生み出すFCFの現在価値の合計」で求められる。
企業価値を高め方
企業価値を高めるポイントは下記である。結局のところ「安く資金を調達し、良い事業に投資を行う。資産は眠らせずに再投資する」に尽きる。
- FCFを高める(収益率を高める、良い事業投資を行う)
- WACCを下げる(資本コストを下げる、安く資金調達する)
- 非事業資産は売却して再投資に回す
- EVA (Economic Value Added)
- 経済的付加価値。単年度でどれだけ企業価値が増加したかを表す。平たく言えば「最終的な利益から配当と利息を引いた値」である。
- ROIC (Return On Invested Capital)
- 投下資本利益率。投下資本に対してどれだけ利益を上げられているかを表す。
投資の決定
銀行、あるいは株主から調達したお金を、「どの事業に投資するのか」を決定する。資金調達にかかったコスト以上の利益を上げられるかどうか、が重要な判断材料となる。
投資判断指標
- NPV法 (Net Present Value)
- 正味現在価値。支払う「価格」よりも「価値」が高いかどうかを判断するための指標。NPVが0よりも大きければ投資すべき。
nは年数、rは割引率。
- IRR法 (Internal Rate of Return)
- 内部収益率。NPVが0になるような割引率(価値と価格がちょうど均衡する割引率)。IRR>WACCならば投資すべき。
資金の調達
銀行、あるいは株主から「どのように資金を調達するか」を決定する。資金調達にかかるコストを「資本コスト」と呼ぶ。銀行からの借入により資金調達する方法と、新株発行により株主から資金調達する方法がある。両者からの借り入れバランスと株主から調達した場合にかかるコストの低減努力が資金調達においては重要となる。
資本コストの算定方法
- WACC (Weighted Average Cost of Capital)
- 加重平均資本コスト。負債コストと株主資本コストの加重平均により算出。負債コストには節税効果があり、その分調達コストが割安になる。
- 負債コスト
- 銀行からの借入にかかるコスト。利息を指す。
- 株主資本コスト
- 株主から資金を調達にかかるコスト。配当を指す。CAPM(Capital Asset Pricing Model)により算出できる。
βは「株式市場の変動に対して、その会社の株式がどれだけ連動するか」を表す。
株主資本コストの下げ方
投資家の求めるリターンは、リスクに応じて高くなる。「リスク」とは「不確実性」であり、「リスクが高い」とは「変動幅が大きい」ことを意味する。つまり、透明性の低い企業(情報開示が適当な企業)は、「リスクが高い」と判断されやすく、株主資本コストが上昇する傾向にある。株主資本コストを下げるには、適切なタイミングで適切な企業情報を公開し、投資家のリスク認識を下げることが重要となる。
資本構成と企業価値・資本コスト
資本構成には下記のようなタイプがある。企業価値を高め、資本コストを下げるには、バランスの取れた負債と株主資本の構成を目指すことが重要である。
- 借金なし
- 借金あり
- 負債多め、株主資本少なめ
- 負債少なめ、株主資本多め
- バランスの取れた負債と株主資本
資本構成と企業価値
「負債なし」に比べ、「負債あり」では負債の節税効果分だけ企業価値が高まる。しかし、負債が増えすぎると倒産リスクが高くなり、倒産した場合に生じる財務破綻コスト分だけ企業価値が低くなる。
\[\begin{align} 企業価値\_{負債あり} =& 企業価値\_{負債なし} \\\\ & + 節税効果 \\\\ & - 財務破綻コスト \end{align}\]資本構成と資本コスト
負債の割合を増やすとWACCは下がる。これは、株主資本コストよりも負債コストの方が低く、節税効果があるためだ。しかし、負債の割合が高すぎるとWACCは上昇に転じる。これは下記「負の連鎖」に起因する。
\[\begin{align} 負債が増える &\rightarrow 格付けが下がる \\\\ &\rightarrow 負債コストが上がる \\\\ &\rightarrow 財務リスクが増える \\\\ &\rightarrow 株主資本コストが上がる \end{align}\]配当政策
成長が鈍化し、NPVが0より高くなるような投資案件がなくなってきたら配当すべき。配当にしても自社株取得にしても、本来はこれから伸びていこうという会社が行うオペレーションではない。
\[配当前の株主価値 = 配当額 + 配当後の株主価値\]- 増配
- 経営者が将来の業績予測を楽観的に見ていることを意味するが、一方で「将来の投資機械がない」というネガティブなシグナルにもなり得る。
- 自社株買い
- 自社株が割安だと考えている証拠であり、将来にわたって安定してキャッシュ・フローを稼ぎ出せるという経営者の自身とも受け止められる。しかし、増配と同様に「将来の投資機械がない」というネガティブなシグナルにもなり得る。
関連知識
その他、この本の中で紹介されている有益そうな知識をまとめておく。また、この本には記載されておらず、自分で計算した理論価格の導出もこちらにメモしておく。
会計とファイナンスの違い
会計とファイナンスの違いを以下に示す。会計は「資金調達とその運用の『結果』」に着目するが、ファイナンスでは「資金調達とその運用の『方法』」に着目する。
| 項目 | 会計 | ファイナンス |
|---|---|---|
| 対象 | 利益 | キャッシュ |
| 時間軸 | 過去 | 未来 |
| 口癖 | 簿記用語 | カタカナ用語 |
将来価値と現在価値
お金の価値は、そのお金をいつ受け取るかで変わる 明日のお金より、いまのお金の方が価値がある
- FV (Future Value)
- 将来価値。今のお金を複利で運用した場合に、将来どれくらいの価値になるか。将来のある時点における価値は、下記式によって求められる。
CFは元本、rは利率、nは年数。
- PV (Present Value)
- 現在価値。お金の価値は時間が進めば進むほど小さくなる。将来のある時点における価値の現在価値は、下記式によって求められる。
CFは元本、rは割引率、nは年数。
理論価格
金融商品の理論価格は、その商品が将来生み出すキャッシュ・フローの現在価値の合計によって求められる。
\[理論価格 \approx \frac{{\rm CF}}{r}\]CFはキャッシュフロー、rは割引率。
理論価格の算出
\[\begin{align} 理論価格 &= \int_0^\infty \frac{{\rm CF}}{\left(1+r\right)^t} dt \\\\ &= {\rm CF} \int_0^\infty \left(\frac{1}{1+r}\right)^t dt \\\\ &= {\rm CF} \left[\frac{(\frac{1}{1+r})^t}{\log{\frac{1}{1+r}}}\right]_0^\infty \\\\ &= \frac{{\rm CF}}{\log{\frac{1}{1+r}}} \left[\left(\frac{1}{1+r}\right)^\infty - \left(\frac{1}{1+r}\right)^0\right] \\\\ &= \frac{{\rm CF}}{\log{(1+r)^{-1}}} (-1) \\\\ &= - \frac{{\rm CF}}{-\log{(1+r)}} \\\\ &\approx - \frac{{\rm CF}}{-r} \\\\ &\approx \frac{{\rm CF}}{r} \end{align}\]理論価格の算出には、下記の数学的な知識を応用した。
- 指数関数の積分
ただし、\(a>0\)
- マクローリン展開
xの値が十分に小さい場合
\[\log{(1+x)} \approx x\]- 対数の性質